🌌 arthurs.dev

Recent Notes

Algorithm Constructs

3 min read

Many problems can be solved using some variation or combination of the same constructs. I think it’s important to drill these constructs (as if learning a musical scale!) so they can practically be performed blind—allowing one to focus on the rather nuanced parts of any given problem.

I’ll be going through these constructions in order of priority (frequency, payoff, and ease of generalization):

Tier 1

A log(n) algorithm that depends on a sorted array A. It works by closing the search space defined as [left, right] (both inclusive) logarithmically.

Your classic ‘find-a-target’

function BinarySearch(A, target):
	left <- 0 # inclusive
	right <- length(A) - 1 # exclusive
	
	while left <= right: # left and right being equal is still a valid search space
		mid <- floor((left + right) / 2) # floor biases towards the left here, but can bias right instead
		
		if A[mid] = target:
			return mid
		else if A[mid] < target # if we must go higher, bump left above mid
			left <- mid + 1
		else: # if we must go lower, demote right below mid
			right <- mid - 1
			
	return NOT_FOUND

‘Feasibility’ search OR (lower/upper)-bound search
For minimizing a maximum, or maximizing a minimum. This pseudocode attempts to find a value that is feasible, then minimizes it as much as possible. What if you tried maximizing the feasible value instead, what would that look like?

function FeasabilitySearch(left, right):
	while left < right: # when left 
		mid = floor((left + right) / 2)
		if feasible(mid):
			# good! now the goal is to minimize this value, so let's discard everything to the right
			right <- mid   
		else: 
			# bad! let's discard everything on the left (including mid) and try again
			left <- mid + 1
			
	return left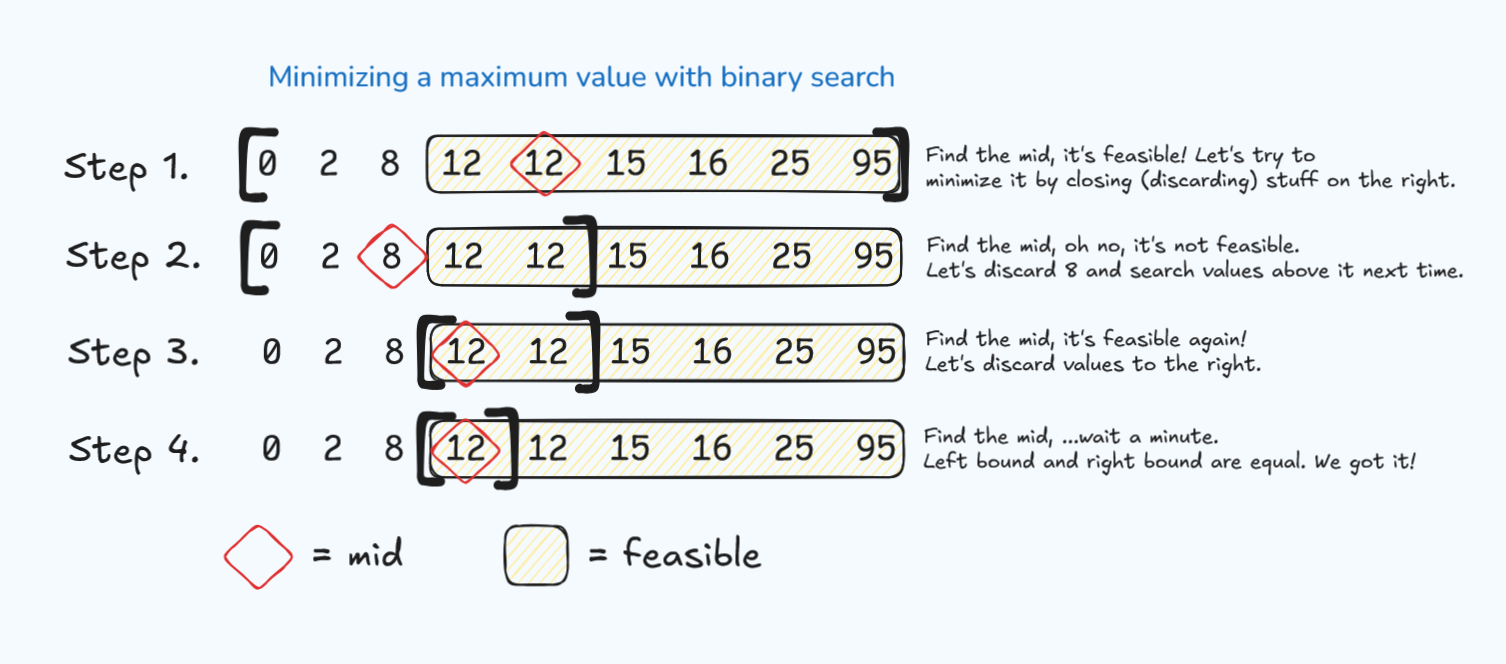

CAVEAT! This assumes a feasible value is guaranteed to be in any provided range, if not, then you’ll find that your left (or right when maximizing) happens to point at whatever could be feasible. If your left ran off the array, well
 it didn’t find anything. So we can check if left == len(arr) to determine if nothing was found.

ANOTHER CAVEAT! When maximizing a minimum you may be faced with bounds that look like this: [2 (feasible), 3 (infeasible)]. If we were to pick a midpoint traditionally → we’d get 2 → move up the left bound → pick a midpoint → 
still get 2 → 
we’re in an infinite loop. It’s important to bias the midpoint in the direction you want to close in on at all times, so we’re going to bias it towards the ceiling: mid <- ceil((left + right) / 2).

YET ANOTHER CAVEAT! Your feasibility function must be monotonic just like your array, extending towards either negative infinity or positive infinity. Otherwise, there’s no point in doing a binary search, that would be like scrambling the order of a dictionary and trying to find your favorite word.

Graph View